برای به دست آوردن معادلات در قاب مرجع متحرک فرض می‌کنیم که یک سیستم دستگاه مختصات نسبت به یک دستگاه مرجع لخت (ساکن) جابجایی خطی با سرعت  دارد و با سرعت زاویه‌ای  می‌چرخد.

در شکل ۱ دستگاه مرجع ساکن و متحرک با جزئیات نشان داده شده است.

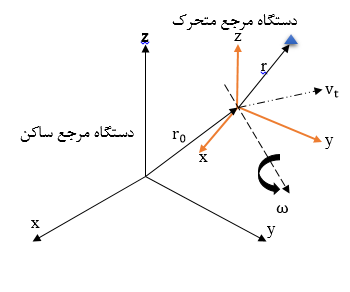
همان‌طور که در شکل مشخص است یک نقطه دلخواه از دامنه محاسباتی توسط بردار مکان   که از مبدا دستگاه متحرک شروع می‌شود، مشخص می‌گردد. مطابق شکل، سرعت سیال می‌تواند از دستگاه ساکن به دستگاه متحرک با استفاده از رابطه زیر انتقال یابد:

(۱)                                                                                                              

در رابطه ۱، v_r سرعت نسبی (سرعتی که از مرجع متحرک دیده می‌شود)، v سرعت مطلق (سرعتی که از دستگاه ساکن دیده می‌شود) و u_r سرعت دستگاه متحرک نسبت به دستگاه مرجع ساکن است و به صورت زیر تعریف می‌شود:

(۲)                                                    

ذکر این نکته ضروری است که هر دو مقدار سرعت خطی و زاویه‌ای دستگاه متحرک می‌تواند تابعی از زمان باشد. هنگامی که معادلات حرکت در قاب مرجع متحرک حل می‌شوند، ترم‌هایی به شتاب سیال اضافه می‌شود که در معادلات مومنتوم ظاهر می‌شوند.

معادلات در این حالت می‌تواند براساس دو فرمولاسیون مختلف نوشته شود. این دو روش شامل استفاده از سرعت‌های نسبی و سرعت‌های مطلق به عنوان متغیرهای وابسته است. نرم‌افزار ANSYS Fluent این قابلیت را به کاربر می‌دهد که در صورت استفاده از حلگرهای Pressure-Based از هر دو فرمولاسیون نسبی و مطلق استفاده کند ولی هنگامی که از حلگر Density-Based استفاده نماید فقط می‌تواند از فرمولاسیون مطلق استفاده کند.

فرمولاسیون سرعت نسبی (Relative Velocity Formulation)

معادلات حاکم برای جریان سیال با در نظر گرفتن فرمولاسیون سرعت نسبی بصورت زیر نوشته می‌شود:

معادله پیوستگی:

(۳)        

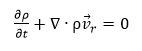
معادله مومنتوم:

(۴)   

معادله انرژی:

(۵)   

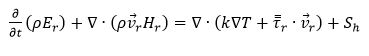
در رابطه ۴، α شتاب زاویه‌ای و a شتاب خطی است که به ترتیب ناشی از تغییرات سرعت زاویه‌ای و خطی دستگاه مختصات متحرک هستند. معادله مومنتوم چهار ترم شتاب اضافی دارد. دو ترم اول به ترتیب شتاب‌ کوریولیس (۲w×v_r ) و شتاب مرکزگرا (w×w×r) هستند. این دو ترم زمانی که مرجع به صورت یکنواخت حرکت می‌کند و یا به صورت متغیر با زمان حرکت می‌کند، ظاهر می‌شود. ترم‌های سوم و چهارم به خاطر تغییرات ناپایای سرعت چرخشی و خطی ایجاد می‌شوند. دو ترم آخر در صورت ثابت بودن سرعت چرخشی و خطی دستگاه مختصات از معادله حذف می‌شوند. t_r (تنش برشی) که در معادله ۴ ظاهر شده است به صورت زیر محاسبه می‌شود:

(۶)   

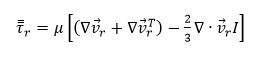
معادله انرژی نیز به فرم انرژی درونی نسبی (E_r ) و آنتالپی کل نسبی (H_r) که روتالپی (Rothalpy) نیز نامیده می‌شود، نوشته می‌شود. این دو کمیت به صورت زیر تعریف می‌شوند:

(۷)  

(۸)

فرمولاسیون سرعت مطلق (Absolute Velocity Formulation)

برای فرمولاسیون سرعت مطلق، معادلات حاکم جریان سیال برای یک مرجع متحرک یکنواخت به صورت زیر نوشته می‌شوند:

معادله پیوستگی:

(۹)    

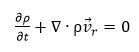
معادله مومنتوم:

(۱۰)   

معادله انرژی:

(۱۱)

در این فرمولاسیون، شتاب‌های کوریولیس و مرکزگرا می‌توانند به صورت یک ترم واحد به فرم  (v-v_t)× wنوشته شوند. دقت شود که در معادله مومنتوم برای فرمولاسیون سرعت مطلق هیچ ترم صریحی برای ترم‌های شامل a و α وجود ندارد.

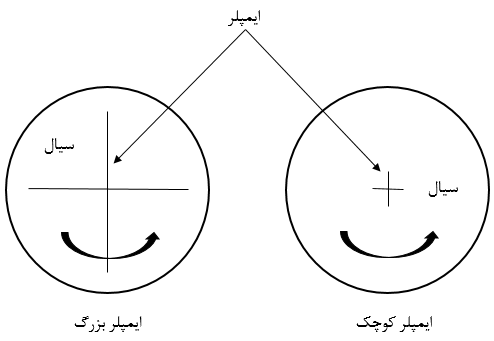
استفاده از فرمولاسیون سرعت مطلق زمانی بهتر است که جریان در بیشتر دامنه حرکت نداشته باشد (مثل یک فن در یک فضای بسیار بزرگ). این در حالی است که استفاده از فرمولاسیون سرعت نسبی برای مواردی مناسب است که اکثر سیال در دامنه در حال حرکت است (مثل یک ایمپلر بزرگ در داخل یک محفظه) (شکل۲).

کلمات کلیدی:

قاب مرجع متحرک، فرمولاسیون سرعت نسبی، فرمولاسیون سرعت مطلق، روتالپی، ایمپلر، فلوئنت، انسیس

Moving Reference Frame, Relative Velocity Formulation, Absolute Velocity Formulation, Rothalpy, ANSYS Fluent, Fluent