بهواسطه پیشرفت سریع فنآوری رایانه و سهولت دسترسی به آن، بکارگیری روشهای عددی عمومیت یافتهاند.
اساس این روشها، شبیهسازی یک محیط با بینهایت درجه آزادی (مانند تودهسنگ) توسط محیطی با درجه آزادی محدود در تعداد معینی از نقاط میباشد. چنانچه اثر نیرو و بارگذاری در این نقاط بررسی شده و پس از آن میزان تغییرشکل در این نقاط تعیین شود، برای سایر نقاط تغییر شکل با روشهای درونیابی محاسبه میگردد. در اغلب این مسائل محیط دارای شکل دلخواه میباشد که تحت بارگذاری ثقلی، نیروهای خارجی، تنشهای برجا، تغییرات درجه حرارت، فشار سیال، پیشتنیدگی و نیروهای دینامیکی قرار گرفته و برای پیداکردن تغییر شکلها از روابط تنش-کرنش در تودهسنگ استفاده میشود. در سالهای اخیر بهمنظور طراحی فضاهای بزرگمقطع، بیشتر از تحلیلهای عددی استفاده شده است.
محیطهایی که یک سازه در آنها و یا بر روی آنها ساخته میشود به سه دسته پیوسته[۱]، ناپیوسته[۲] و شبهپیوسته[۳] قابل تقسیم هستند. </p
شکل (۱) طبقه بندی زمین را در حالتهای مختلف نشان میدهد.
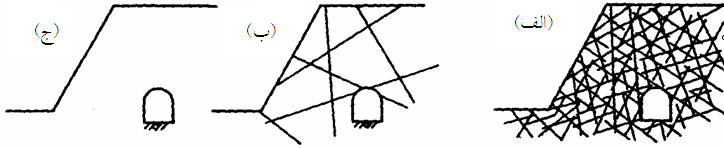
شکل (۱) طبقه بندی زمین: (الف) نوع پیوسته، (ب) نوع ناپیوسته و (ج) نوع شبه پیوسته
نوع اول ممکن است برای زمینهایی که از سنگ بکر بدون درزه و شکاف تشکیل شدهاند، بکار روند. نوع دوم نماینده سنگهای درزهدار است و نوع سوم برای سنگهایی است که شدیداً خرد شده و یا هوازده هستند. بهدلیل آنکه رفتار نهایی زمینهای نوع سوم میتواند شبیه به رفتار زمینهای نوع اول باشد، رفتار این زمینها را شبه پیوسته مینامند. رفتار مکانیکی نوع اول بهکمک تئوری مکانیک محیط پیوسته قابل تحلیل است، در حالیکه برای تحلیل رفتار زمینهای نوع دوم باید از تئوریهای مربوط به محیطهای ناپیوسته استفاده شود. برای تحلیل رفتار نوع سوم میتوان از تئوریهای محیطهای ناپیوسته استفاده کرد. ولی از آنجا که تعیین موقعیت، ابعاد و خواص مکانیکی همه سیستمهای درزه غیرممکن بهنظر میرسد، بر این اساس، درعمل روش تحلیل محیطهای ناپیوسته برای تحلیل رفتار این نوع محیطها کاربرد عملی نخواهند داشت. با توجه به اینکه این زمینها تا حدی شبیه به محیطهای پیوسته رفتار میکنند، میتوان از تئوری محیطهای پیوسته برای تحلیل رفتار آنها استفاده کرد. باید در نظر داشت که تاثیر ناپیوستگیها بهصورت مناسبی در مدلسازی زمینهای نوع سوم بهعنوان یک محیط پیوسته منظور شود. این فرآیند باعث ایجاد مدل پیوستهای معادل با تودهسنگ ناپیوسته و درزهدار خواهد شد. با درنظر گرفتن مطالب بالا، زمینهای پیوسته و شبهپیوسته را میتوان بهعنوان اجسام پیوسته درنظر گرفت، در حالیکه زمینهای ناپیوسته بایستی با نهایت دقت ممکن و با درنظر گرفتن همه درزهها بهطور جداگانه، در یک مدل ناپیوسته مدل شوند. بعد از مدلسازی زمین، همه مقادیر ثابتهای مکانیکی و هندسه درزهها را میتوان با استفاده از تحلیل برگشتی تعیین نمود. به دلایل زیر روشهای عددی بر سایر روشها برتری دارند:
– با استفاده از روشهای عددی، هر سازه با هر شکل سطح مقطعی را میتوان تحلیل نمود.
– با استفاده از روشهای عددی میتوان تنش و جابجایی را بهراحتی در تمام نقاط سیستم و در هر زمان که لازم باشد بهدست آورد.
– در روش عددی میتوان روند حفاری، نصب، نگهداری و سایر فعالیتهای تونلسازی را درنظر گرفت.
در روشهای عددی میتوان ناهمگنیها، مناطق درزهدار، گسلها و لایههای مختلف زمین را در مدل لحاظ نمود.
همچنین میتوان خواص مصالح را بصورت غیرخطی درنظر گرفت و یا حتی جریان آب زیرزمینی را نیز شبیهسازی کرد.
اغلب محیطهای سنگی که در آنها فضای زیرزمینی احداث میشود دارای محیطی پیوسته نبوده و بهدلیل وجود دستهدرزهها محیطی ناپیوسته محسوب میشوند. با وجود مزایای بسیار، تکنیکهای شبیهسازی رایانهای محدودیتهای قابل توجهی نیز دارند. چنانچه خواص فیزیکی و مکانیکی تودهسنگ برجا بهطور دقیق مشخص نباشد، شبیهسازی کامپیوتری نمیتواند نتایج معتبری ارائه دهد. بعد از حفر تونل، خواص فیزیکی و مکانیکی تودهسنگ تغییر میکند. بنابراین با بکارگیری پارامترهای بهدست آمده از برآوردهای آزمایشگاهی نمیتوان رفتار تودهسنگ را بهخوبی پیشبینی کرد. بهدلیل عدم توانایی در شبیهسازی تمام زمین و یا حتی تمام یک مجموعه حفاری، تنها بخشی از زمین مدلسازی شده و با توجه به مدل مفروض، شرایط مرزی برای مدل مورد نظر تعریف میشود. بهمنظور از بینبردن این مرزها در تحلیل تنش، کرنش و تغییر شکل در اطراف یا در امتداد تونل، مرزها بهقدر کافی دور از تونل درنظر گرفته میشوند که در نتیجه باعث افزایش تعداد المانها میشود.
در حال حاضر در حل مسائل ژئوتکنیک کاربرد پنج روش عددی زیر بسیار رایج است:
۱- روش المان محدود [۴](FEM)
۲- روش تفاضل محدود [۵](FDM)
۳- روش المان مرزی [۶](BEM)
۴- روش المان مجزا [۷](DEM)
۵- روش تغییر شکل ناپیوسته [۸](DDA)
مراحل مدلسازی تونل:
انتخاب محدوده مناسبی از تودهسنگ
در اولین مرحله از مدلسازی باید شبکهای مناسب برای مسئله تعریف شود و بدین ترتیب تعداد المانها در مدل مشخص میشود. در این مرحله باید المانها با ابعاد مناسب وارد شوند. در این مرحله اگرچه میتوان با افزایش تعداد المانهای شبکه نتایج دقیقتری را بهدست آورد اما باید دقت داشت که با افزایش تعداد المانهای شبکه، سرعت حل کندتر خواهد شد و با محدودیت حافظه در رایانه مواجه خواهیم شد. بنابراین ایده اول در این زمینه مربوط به حل دقیق ریاضی در محیطهای کشسان و الاستیک (روابط کرش) میباشد که حداکثر ناحیه تاثیر یک حفره زیرزمینی تا سه برابر قطر آن برآورد شده است. بدین ترتیب در صورتیکه تودهسنگ بهصورت الاستیک رفتار نماید در فاصله سه برابر قطر، تنشها به وضعیت اولیه خود میرسند. از طرف دیگر با توجه به این نکته که اگر ابعاد مدل حدود ۱۰ برابر ابعاد حفره باشد، تحت شرایط مرزی متفاوت درصد خطاها به حداقل ممکن (حدود %۰/۵) کاهش خواهد یافت .
انتخاب مدل رفتاری مناسب و تعیین پارامترهای آن
بسته به شرایط مسئله و نوع محیط مدل میتوان از مدلهای رفتاری مختلفی که در نرمافزارهای مدلسازی عددی در نظر گرفته شده است استفاده نمود. از میان مدلهای رفتاری مختلفی که در این نرمافزار پیشنهاد میشوند، مدل رفتاری موهر- کلمب مدل مناسبی برای تودهسنگ و خاک است. مدل رفتاری موهر- کلمب نمایانگر موادی است که تنها در اثر برش به حد تسلیم میرسند و در مکانیکسنگ و خاک برای حالت پلاستیک مدل مرسومی است. با انتخاب هر کدام از مدلهای رفتاری جهت استفاده در مسئله، پارامترهایی که لازمه بکارگیری آن مدل رفتاری است باید مشخص شود. پارامترهای هر مدل با هر مدل دیگری متفاوت است. مثلاً در مدل الاستیک احتیاج به سه پارامتر مدول حجمی، مدول بالک و دانسیته میباشد در صورتی که در مدل موهر- کلمب علاوه براین سه پارامتر نیاز به تعیین سه پارامتر دیگر چون چسبندگی، زاویه اصطکاک داخلی و مقاومت کششی تودهسنگ یا خاک میباشد.
بنابراین باید قبل از مدلسازی، هر کدام از پارامترهای مذکور بسته به نوع منطقه با انجام یک سری آزمونهای برجا یا آزمایشگاهی تعیین شود و اصولاً دقت نتایج حل یک مدل در دقیقبودن پارامترهای مختلف بهدست آورده شده در منطقه است. لازم بهذکر است مدول حجمی (K) و مدول برشی (G) بر اساس روابط زیر برای تودهسنگ محاسبه میشوند.

اعمال شرایط مرزی و تنش های اولیه
در این مرحله باید شرایط مرزی و یا تنشهای اولیه به مدل اعمال شود.
معمولاً در شرایط مرزی تعیین وضعیت جابجاییها و یا تنشها در مرز مدل کار مشکلی است.
لذا با توجه به اینکه مقدار دقیق تنشهای برجا مشخص نیست، ثابتکردن مرز مدل بهنحویکه جابجایی نقاط مرزی صفر باشد تنها راه اعمال شرایط مرزی واقعی است.
حل مدل تا رسیدن به تعادل قبل از حفاری
دراین مرحله سعی میشود با الگو گرفتن از آنچه در واقعیت اتفاق میافتد شرایط مدل به واقعیت نزدیکتر شود. در حفر تونل واقعیت این است که قبل از حفر تونل، زمین در حال تعادل است و حفر تونل باعث به وجود آمدن یک سری اغتشاشات در وضعیت تنشها و جابجاییها خواهد شد. با توجه به اینکه تا این مرحله شرایط مرزی و تنشهای برجا در مدل اعمال شدهاند، لازم است مدل عددی قبل از حفر تونل حل شود تا تنشهای اولیه ایجاد شوند. همچنین قبل از ایجاد هر نوع حفره، لازم است جابجاییها صفر شوند تا شرایط مرزی واقعی قبل از حفر تونل منظور گردد.
حفر تونل و حل مدل تا رسیدن به تعادل
پس از واقعی ساختن شرایط تنشها و صفرکردن جابجاییها، تونل با هندسه مربوطه در مدل ایجاد میگردد. بسته به اینکه حل مدل با نصب سیستم نگهداری و یا بدون نصب سیستم نگهداری مدنظر باشد، شرایط متفاوت خواهد بود. بدین معنی، در حالتی که نصب سیستم نگهداری مدنظر نباشد، حل مدل تا رسیدن به تعادل کامل ادامه خواهد یافت. اما اگر نصب سیستم نگهداری مدنظر باشد باید سیستم نگهداری در یک فاصله زمانی پس از حفر صورت گیرد تا مدلسازی هرچه بیشتر با واقعیت تطبیق یابد.
بدین ترتیب در این حالت مدل پس از حفر تا رسیدن به تعادل قبل از نصب سیستم نگهداری حل میشود.
اعمال ترخیص تنش
قبل از حفر تونل، زمین تحت فشار ناشی از تنشهای طبیعی قرار دارد. هرگونه حفر این وضعیت تنش را بههم زده و باعث جابجاییهایی در زمین میگردد. بهطور کلی همگرایی همیشه پیش از رسیدن سینهکار به مقطع مورد نظر آغاز میشود. در این مورد معمولاً محل شروع همگرایی را از فاصلهای حدود نصف عرض فضای زیرزمینی تا مقطع مورد نظر تخمین میزنند. البته پس از عبور سینهکار از مقطع مورنظر سرعت همگرایی بیشتر میشود. برای تشریح بهتر این مسئله یک تونل دایرهای حفرشده در محیطی همگن، همسانگرد و تحت تنشهای هیدروستاتیک (![]() ) که قرار است با یک پوشش بتنی نگهداری شود، مفروض است. برای تبدیل مسئله به حالت دوبعدی، فرض میشود که تونل در زمان کوتاه و در طولی نامحدود حفرشده و همچنین قسمت تخلیهشده با یک فشار داخلی اعمالی به دیواره تونل جایگزین شود. اگر مقدار این فشار (P) با تنش طبیعی زمین (<
) که قرار است با یک پوشش بتنی نگهداری شود، مفروض است. برای تبدیل مسئله به حالت دوبعدی، فرض میشود که تونل در زمان کوتاه و در طولی نامحدود حفرشده و همچنین قسمت تخلیهشده با یک فشار داخلی اعمالی به دیواره تونل جایگزین شود. اگر مقدار این فشار (P) با تنش طبیعی زمین (<![]() ) که پیش از حفر تونل وجود داشته است برابر باشد، هیچگونه همگرایی بهوجود نخواهد آمد. اما با کاهش فشار داخلی (P) زمین دربرگیرنده، تونل تحت جابجایی قرار گرفته و دیواره تونل به سمت داخل حرکت میکند که به آن همگرایی گفته میشود.
) که پیش از حفر تونل وجود داشته است برابر باشد، هیچگونه همگرایی بهوجود نخواهد آمد. اما با کاهش فشار داخلی (P) زمین دربرگیرنده، تونل تحت جابجایی قرار گرفته و دیواره تونل به سمت داخل حرکت میکند که به آن همگرایی گفته میشود.
این میزان کاهش فشار، ترخیص تنش (SR) نامیده میشود.
بهجای استفاده از متغیرP میتوان از نسبت ![]() تحت عنوان ضریب محصوریت و یا متغیر
تحت عنوان ضریب محصوریت و یا متغیر ![]() موسوم به ضریب آزادی استفاده نمود.
موسوم به ضریب آزادی استفاده نمود.
ضریب آزادی برابر است با:
![]()
که در این رابطه ![]() جابجایی شعاعی تونل در نقطهای به فاصله r از مرکز تونل است، که با استفاده از رابطه زیر بهدست میآید.
جابجایی شعاعی تونل در نقطهای به فاصله r از مرکز تونل است، که با استفاده از رابطه زیر بهدست میآید.

</p</p
که در این رابطه R شعاع تونل میباشد.
در یک حالت خاص، با جاگذاری R = r همگرایی روی دیواره تونل حاصل میشود.
جابجایی در نقطهای با فاصله بینهایت از مرکز تونل نیز با ![]() نشان داده میشود. برای محاسبه درجه آزادی میتوان از شکل (۲) که طرح کلی سینهکار در حال پیشروی است، الگو گرفته و از نمودار شکل (۳) که توسط پنت در سال ۱۹۹۵ ارائه شده است استفاده نمود.
نشان داده میشود. برای محاسبه درجه آزادی میتوان از شکل (۲) که طرح کلی سینهکار در حال پیشروی است، الگو گرفته و از نمودار شکل (۳) که توسط پنت در سال ۱۹۹۵ ارائه شده است استفاده نمود.
در این نمودار مقدار جابجایی نرمال شده بر حسب فاصله از سینه کار از رابطه زیر قابل محاسبه است:
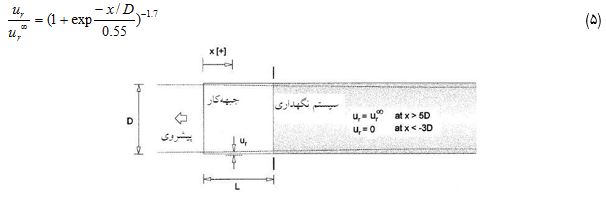
شکل (۲) طرح کلی سینهکار در حال پیشروی
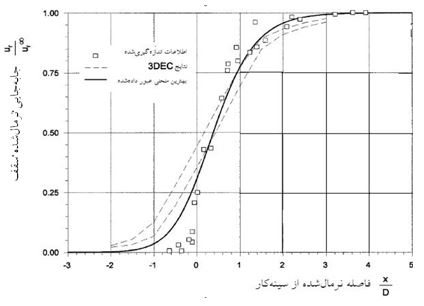
</p
شکل (۳) تغییرات روند جابجایی بر حسب فاصله از سینه کار
همانطور که در شکل (۴-۴) مشخص شده، در این رابطه x گام پیشروی و D قطر تونل میباشد.
با توجه به اینکه محیط دربرگیرنده تونل در مقطع مورد بررسی ضعیف بوده، لذا مقدار گام پیشروی براساس شرایط اجرایی برابر یک درنظر گرفته شده است.
لذا با محاسبه نسبت x/D و مکانیابی آن روی نمودار شکل (۳) مقدار متناظر ![]() بهدست میآید.
بهدست میآید.
تخمین سیستم نگهداری
تخمین سیستم نگهداری مورد نیاز برای پایدارسازی تونل به کاهش مقاومت وابسته به زمان در سنگها، توزیع مجدد سهبعدی نیروهای اطراف حفاری و طبیعت غیرقابل اطمینان سنگ تا زمانی که تحت تاثیر سینهکار است، بستگی دارد. وقتی سیستم نگهداری در نزدیکی سینهکار نصب میشود، همه بار روی این سیستم منتقل نمیشود، بلکه قسمتی از بار که در اطراف فضای حفاری توزیع مجدد یافته، توسط خود سینهکار تحمل میشود.
با پیشروی تونل، تاثیر سینهکار کاهش یافته و سیستم نگهداری باید مقدار بیشتری از بار را تحمل کند.
لحاظ نمودن وقفه زمانی بین حفر تونل تا نصب نگهداری، تاثیر بسزایی در کاهش حجم تزریقهای تحکیمی دارد.
چرا که بخش قابل توجهی از تغییر شکل تودهسنگ در همین فاصله زمانی رخ داده و در اثر این تغییر شکل بخش عمدهای از تنشهای القایی رها شده و درنهایت فشار وارد بر سیستم نگهداری کاهش مییابد.
اگر در مدل عددی به این فاصله زمانی توجه نشود، مسلماً نبایستی انتظار جواب قابل قبول از آن را داشت.
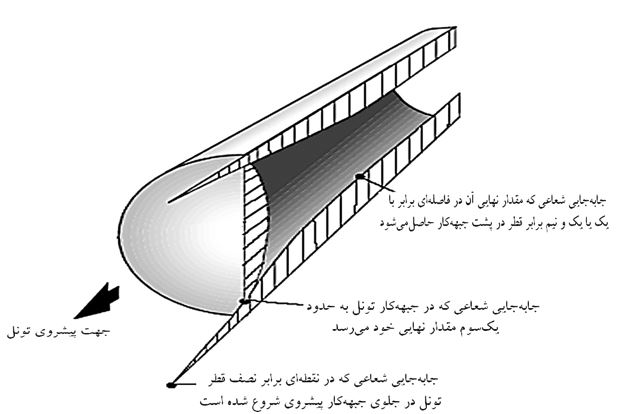
</p</p
شکل (۴) الگویی از تغییرات تودهسنگ مجاور تونل درحال پیشروی
بدین ترتیب میتوان جابجایی را بهعنوان پارامتر کنترلی وقفه زمانی در نظر گرفت.
بدیهی است مقدار آن باید بهنحوی تعیین شود که از جابجایی قابلقبول که از روابط ساکورائی محاسبه میشود، بیشتر نشود.
مقدار این جابجایی به خواص مکانیکی تودهسنگ، وضعیت تنش منطقه و شکل فضای زیرزمینی بستگی دارد.
بررسی پایداری فضای حفاری تا قبل از نصب پوشش اولیه
برای ارزیابی پایداری فضای حفاری لازم است تا نتایج جابجاییهای حاصل از مدل عددی با جابجاییهای مجاز حول فضای زیزمینی مقایسه شوند. در صورتی که این جابجاییها از جابجایی مجاز بهواسطه رابطه (۶) که به عنوان مبنای طراحی نگهداری فضاهای زیرزمینی توسط ساکورائی ارائه شده است، کمتر شود، تونل پایدار خواهد بود.
رابطه کرنش بحرانی در حالت فشاری محصورشده در اطراف تونل را برحسب مدول الاستیسیته محیط بیان میکند.
![]()
</p</p
در این رابطه E مدول تغییر شکلپذیری تودهسنگ برحسب کیلوگرم بر سانتیمتر مربع و ![]() کرنش بحرانی برحسب درصد میباشد.
کرنش بحرانی برحسب درصد میباشد.
با تعیین کرنش مجاز و با استفاده از رابطه (۷) جابجایی مجاز مشخص میگردد.
![]()
</p
که در این رابطه ![]() جابجایی مجاز برای مدل ایجادشده و a شعاع تونل بر حسب متر است.
جابجایی مجاز برای مدل ایجادشده و a شعاع تونل بر حسب متر است.
[۱]. Continuous
[۲]. Discontinuous
[۳]. Pseudo- Continuous
[۴] . Finite Element Method
[۵] . Finite Difference Method
[۶] . Boundary Element Method
[۷] . Distinct Element Method
[۸] . Discontinuous Deformation Analysis

